Vectors

Need to study vectors in Physics

Physics is essentially determination of physical quantities. Physical Quantities are of two types– scalar or vector.

Scalar quantities

Certain physical quantities like distance, speed, density, pressure, temperature, energy, electric current can be expressed by only a number (value or magnitude) with unit ( remember chapter on unit and dimension). Such quantities are called scalar quantities.

For example, speed of any moving object can be expressed as 5 m/s where 5 represents magnitude or value of speed and m(eter)/s(econd) is unit of speed. Similarly if there is pressure of $2 N/m^2 $ on any surface, then 2 is magnitude of that pressure and $N(ewton)/m(eter)^2 $is unit of pressure.

Good thing about scalar quantities are that you can add and subtract them like any numerical value. You just need to take care that units are same.

Energy is a scalar quantity. Energy is measured in Joules. So, if an object has energy of 5 J and it gets another 2 J of energy from heat or any other source, it shall have total of 7 J ( 5 J + 2 J).

Vector quantities

To express physical quantities like displacement, velocity, acceleration, momentum, force, electric field strength etc. one needs not only a scalar value ( magnitude and unit ) but also a direction. Such quantities are called vector quantities.

Velocity as opposed to speed has magnitude as well as direction. For example, we would say, a car is going with a velocity of 2 m/s in North direction. If another car is going at 2 m/s in South direction then its velocity is different from the first even when speed is same. In fact it is negative of first car’s velocity ( yes, unlike speed velocity can have negative value).

Vectors are represented by a symbol with an arrow above it. \(\vec{A}, \vec{a}, \vec{x_1}\) are all valid representations of vectors. Magnitude is represented as the symbol of vector without arrow. For example, symbol for magnitude of vector $ \vec{A} $ is A. Another notation of manitude is $ \lvert\vec{A}\rvert $. Vector with magnitude of 1 is called unit vector. Unit vector is represented as symbol with a hat like $ \hat{i} $.

If direction of vector is reversed, its value becomes negative of original value. It’s magnitude does not change since magnitude is always a positive quantity.

Representing direction

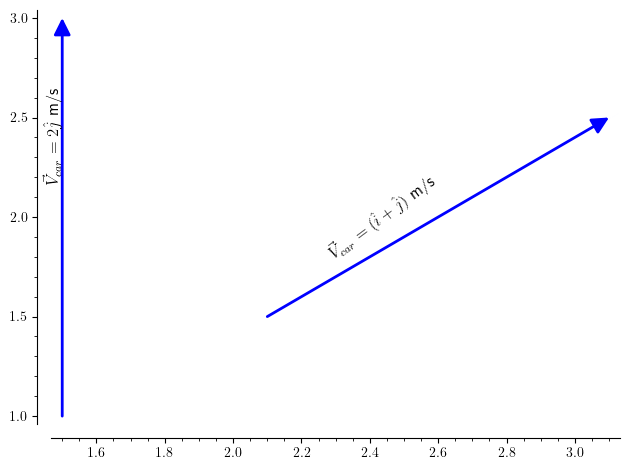
Representing direction in north and south etc. is cumbersome and unscientific. Instead we draw a reference coordinate system which has three axes X-Y-Z (2 axes in case of two dimensions X-Y) which have fixed directions in space. Direction of every vector in terms of direction of the fixed axes, which are in turn represented by unit vectors $ \hat{i} $ for X, $ \hat{j} $ for Y, $\hat{k}$ for Z. So, in our example, when car is travelling in north direction with speed 2 m/s, if we assume that Y axis is pointing in direction of north ( you can assume X axis also). If symbol for velocity of the car is $ \vec{V_{car}} $ then, \(. \vec{V_{car}} = 2 \hat{j} \: m/s\) We can actually represent any direction using linear combination of $ \hat{i}, : \hat{j}, : and :\hat{k} $. For example, if Y axis represent north and X axis represent east then $ \hat{i} + \hat{j} $ shall point in north-east direction.

It shall be clear when we learn how to add (or subtract) vectors.

Addition and subtraction of Vectors

While scalar quantities can be added or subtracted like any number, vector quantities can be added as vectors only.

If two vectors have same direction, their sum would have same direction and magnitude equal to sum of their magnitudes. \(\begin{align} \vec{A} &= A \hat{r}\\\ \vec{B} &= B \hat{r}\\\ \vec{C} &= \vec{A} + \vec{B} \\\ &=A\hat{r} + B\hat{r}\\\ &= (A + B) \hat{r} \end{align}\)

however if they are not in same direction magnitude of sum of vectors would be less than sum of magnitudes. In fact it depends on cos of the angle between two vectors as you shall see later.

It is worthwhile to understand addition and subtraction of vectors as we would frequently need to add vector physical quantities like Force.

To add vectors, vectors need to be arranged so that tail of the second vector should begin from head of the first vector and resultant vector shall begin from tail of first vector and end at head of second vector. One can see it as follows:

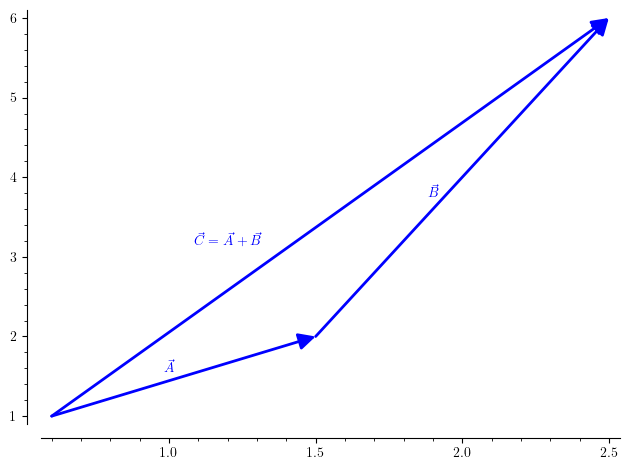
Subtraction is achieved by taking negative of second vector(reversing the direction) and adding: \(\begin{align} \vec{C} &= \vec{A} - \vec{B} \\\ &= \vec{A} + (-\vec{B}) \end{align}\)

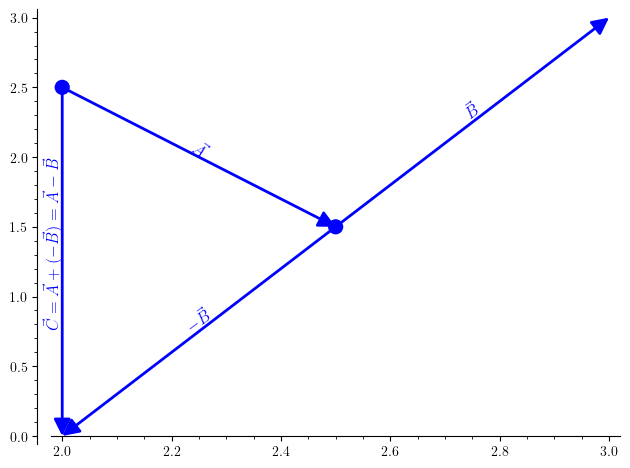
One can see that value of vector does not depend on choice of starting or endpoint but only length and direction of arrow. Therefore, a vector can be moved anywhere if its length and direction do not change.

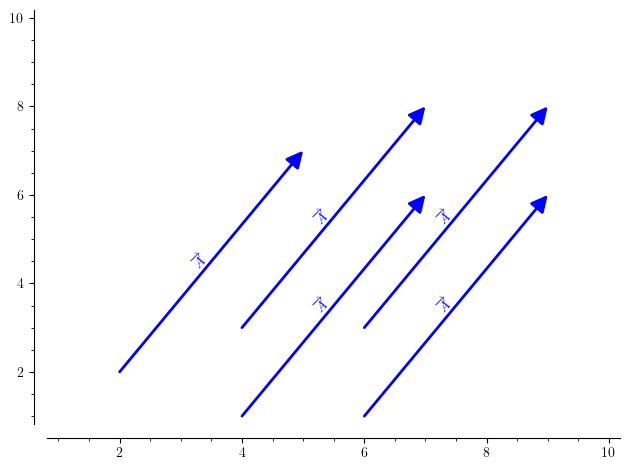
Since, direction remain same, shifted vector is parallel to original one and has same magnitude, a parallelogram is formed if we join heads and tails respectively as follows:

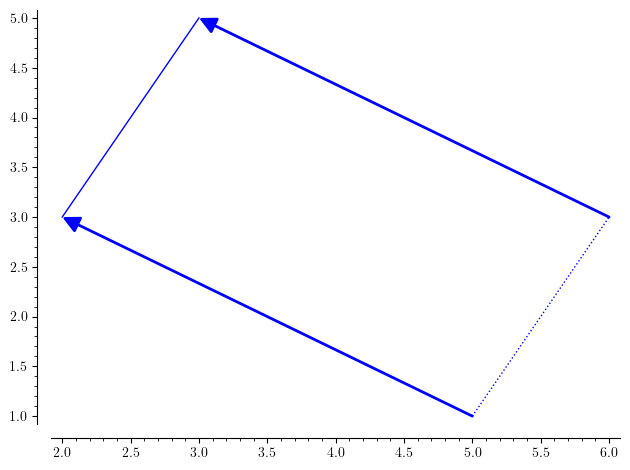
The above property is useful in addition and subtraction if vectors are not drawn such that their head and tail do not coincide.

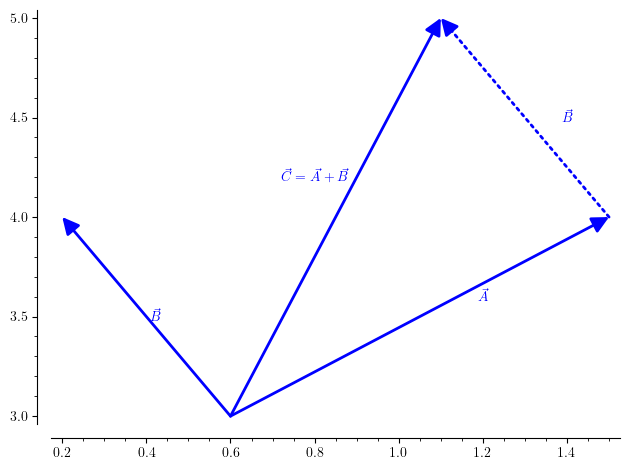Please see that vector has been shifted parallel to its original position keeping magnitude same by forming a parallelogram so that its tail coincides with head of $ \vec{A} $.

X-Component, Y-component of vectors

Each vector can be represented as sum of orthogonal(perpendicular) vectors. Let’s us see first two dimensions but it also applies to 3 dimensions.

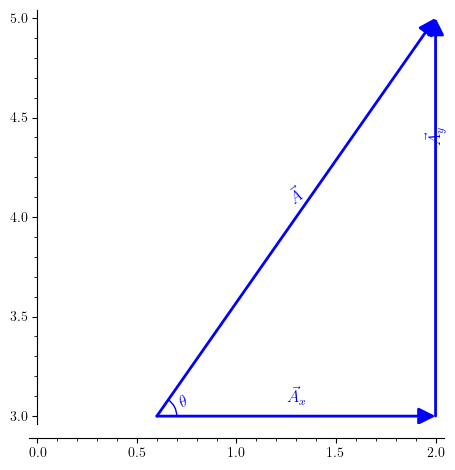
From the image above, one can see that by law of vector addition: \(\vec{A} = \vec{A}_x + \vec{A}_y \tag{1}\) \(\vec{A}_x = A_x \hat{i} \tag{2}\) as $\vec(A)_x$ is towards +X axis. Similarly, \(\vec{A}_y = A_y \hat{j}\tag{3}\) as $\vec(A)_y$ is towards +Y-axis. From (1), (2) and (3) \(\vec{A} = A_x\hat{i} + A_y \hat{j}\) Component of A along X-axis $A_x$ is called X-component.Component of A along Y-axis $A_y$ is called Y-component.

$A_x$ and $A_y$ and $A$ form right angled triangle. Therefore, \(A_x = A\cos(\theta)\\\ A_y = A\sin(\theta)\) Therefore, we can write,

$ \vec{A} = A\cos(\theta)\hat{i} + A\sin(\theta)\hat{j} $

Advantage of breaking vectors into X and Y components is that one can add/substract magnitudes in X and Y components independently of each other and then combine results. This way any 2D problems can be broken into two one dimensional problems.